Information Theory

Information Storage

訊號分成 analog 跟 digital

大致討論的結果(只記得這些…)

type	pros
digital	電腦可讀可驗證易編輯
analog	能保存較原始資料

2000年後 digit 資料量爆炸性成長

Information Value

More Information?

左邊還是右邊給我們比較多的資訊???

幾乎大家一致認同左邊

但那是因為左邊是我們認得的語言

想像如果右邊是另一種語言

可能不同的音調、個數、行數等等都代表不同意義

這樣右邊會不會也是能帶給我們跟左邊一樣的資訊量呢🤔🤔🤔

Measure Information value

那我們又如何衡量資訊的價值呢?

試問下面三個投擲硬幣的結果
那一個sequence比較有價值?

Hint : 隨便挖掉其中一個擲硬幣的結果，你有辦法填回去嗎?

明顯的two-head coin 我們可以直接填H回去

weighted coin 我們會猜H(H 出現機率比較大)

而fair coin 我們就無法做出猜測

Information Entropy

disorder, unpredictability, uncertainty of information

(記得高中老師說熵就是亂度

以下的計算皆以密碼為例

可用字元 b 個
密碼長度 n 個

可用密碼數(combinations)

$$
b^{n}
$$

存儲密碼所需要的位元數(bits of entropy)

$$
\log{b^{n}}
$$

Shannon Entropy( Entropy of given set of characters)

整串密碼中每個字的平均消息量
How many questions would we expect to ask to find an element from a set of characters?
char出現時所需要問的次數的期望值
= 每個char出現的機率 * 出現時所需要問題次數
formula

$$
H(X) = E[I(X)] = E[-\ln(P(X))]
\
H(X) = \Sigma{P(x_i)I(x_i)} = - \Sigma{P(x_i)\log_b{P(x_i)}}, b = 2
$$

implement

Shannon Entropy in ruby

def entropy (str)
  e = 0
  sz = str.bytesize.to_f
  b = str.bytes
  0.upto(255) do |i|
    x = b.count(i)/sz
    if x > 0
      e += - x * (Math.log(x)/ Math.log(2))
    end
  end
  e
end

但當我們在用Shannon Entropy下去對密碼做分析的話

password type	sample password	bits of entropy	Shannon Enrtopy
length = 8, lowercase letters only	cvobmsla	37.60	3.0
length = 8, lowercase + uppercase letters	jAcieDlq	45.60	3.0
length = 8, letters + digits	bA29Fs4f	47.63	3
whole words (4 words chosen at random from 2048 word dictionary)	placidmealerrorpast	44	3.53

增加了char，密碼變的更複雜，但似乎沒有增加enyropy

反而是原先認為容易被字典攻擊法攻擊的whole word 表現不差

而且雖然英數字組合的bits of entropy高，但人類不會偏好隨機的組合

因此實際會被用的組合數還要再下修

反觀whole word的組合數就是真實中的problem space -> 沒有捷徑猜密碼

People who don’t understand information theory and security

別期待user會使用隨機組合的密碼

(譯: 過去二十年，我們努力讓每個人用人類更難記，但電腦很好猜的密碼)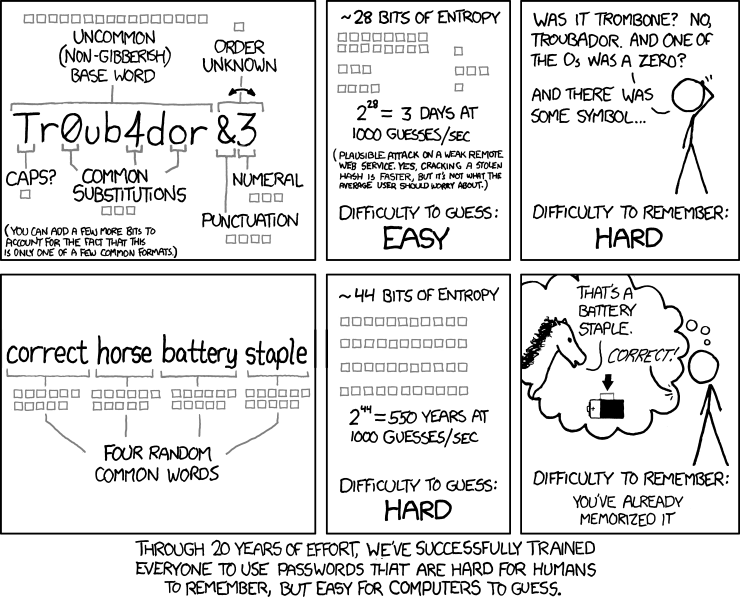

後面是開發環境介紹跟一些bit operation

我就略過

但要特別筆記一下XOR

真值表大家都會記

重點是xor有這個特質

$$
P \oplus K = C
\
C \oplus K = P
$$

這個magic讓xor在一些地方有神奇功用

例如

兩數互換不用第三個變數

void swap(int *a, int *b){
  if(*a != *b) {
      *a = *a ^ *b;
      *b = *a ^ *b;
      *a = *a ^ *b;
  }
}

One-time Pad Cipher(week4)
某天寄來的code challenge

implements function

xor product(N,M) = N ^ N+1 … ^ M-1 ^ M

要求

complexity O(log(N))

mem space usage O(1)

其實看到log(N)就大概想應該是要binary下去找

後來看到一個解法

令f(n) = xor product(0,n)

發現有規律

0000 <- 0 [a]

0001 <- 1 [1]

0010 <- 3 [a+1]

0011 <- 0 [0]

0100 <- 4 [a]

0101 <- 1 [1]

0110 <- 7 [a+1]

b(n) 用來查表求出 xor product(0,n) 跟 xor product(0,m)

兩個再做xor 就會變成 xor product(n,m)

SS-week2